Presumably, the ``Schrodinger equation" in the problem statement refers to the time-independent Schrodinger equation in one dimension, which is given by
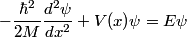 First, we compute the second derivative of 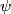 . .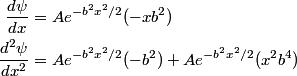 We plug this into the Schrodinger equation to find that 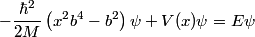 Now evaluate the above equation at 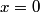 to find that to find that 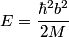 Now plug this back into the Schrodinger equation. 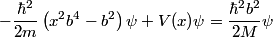 Divide through by 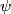 to find that to find that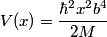 Hence, answer (B) is correct. |